Fluid-Solid Interaction (FSI)
Numerical simulation of fluid-solid interaction (FSI) is crucial for understanding complex behaviors in various engineering and scientific fields. FSI involves the interaction between fluids (liquids and gases) and solid structures, which is essential in many applications such as aerospace, Mechanical and Civil engineering, biomechanics, and environmental sciences. Understanding these interactions helps in predicting how structures will respond to dynamic fluid forces, ensuring safety, performance, and efficiency.
In the design of aircraft and spacecraft, predicting how air interacts with wings and fuselage shapes is vital for optimizing aerodynamic performance. In addition, FSI simulations help assess the impact of wind loads on tall buildings or the effects of waves on offshore structures, guiding safety and design improvements. Besides, understanding blood flow around arteries and valves is key in designing medical devices and treatments for cardiovascular diseases. Moreover, simulating river dynamics and sediment transport aids in flood management and ecological studies, influencing policy and urban planning.
Recent advancements in computational power and algorithm development have significantly enhanced the capabilities of FSI simulations. High-performance computing (HPC) allows for more complex and detailed models, accommodating non-linear behaviors and complex geometries. Machine learning techniques are increasingly being integrated to optimize simulations and predict outcomes more efficiently, reducing computation times.
Moreover, advancements in coupling techniques, such as partitioned and monolithic methods, have improved the accuracy and stability of simulations, allowing for better modeling of fluid-structure interactions across various scenarios.
Typical Numerical Approaches
Computational Fluid Dynamics (CFD): CFD methods simulate fluid motion and are integral for analyzing fluid behavior around solids. Commonly used for solid mechanics, FEM is effective for analyzing the deformation of structures under fluid loads.
Boundary Element Method (BEM): BEM can be advantageous for problems with infinite domains, reducing dimensionality and computational costs.
Smoothed Particle Hydrodynamics (SPH): A Lagrangian method suited for complex fluid flows, SPH is particularly useful in simulations involving free surfaces and interacting fluids.
Problem Definition
This example simulates the motion of a “rocket paper,” a conceptual model representing a simplified rocket, as it navigates a predefined curved path through the air. The simulation seeks to analyze the intricate fluid dynamics surrounding the rocket, emphasizing vortex formation, velocity profiles, and the dynamics of fluid-solid interactions. To effectively capture these phenomena as the body moves over time, it is essential to implement an appropriate moving mesh strategy in conjunction with a robust fluid-solid interaction method. This approach will enable us to accurately simulate the complex behaviors and influences involved in the aerodynamic performance of the model.


Assumptions
The motion of a paper rocket in the air is simulated here based on the following cases and their related assumptions:
- Case A: The rocket’s trajectory is defined as a function of time. In this case, the solid part of the rocket interacts with the air only.
- Case B: The initial velocity of the rocket is known, and its motion is determined by solving the governing equations derived from the dynamics of the solid body, along with the mass and momentum equations for the fluid. This problem is quite complex due to the mutual interactions between the fluid and the solid, which result in a set of fully coupled, nonlinear equations (the results of this case will be presented soon).
Computational aspects
– Fluid-Solid Interaction: To accurately model the interaction between the solid rocket structure and the surrounding airflow, it is essential to implement advanced numerical methods that ensure a precise representation of the forces and motion involved. This involves not only simulating the fluid dynamics around the rocket but also effectively capturing the complex behavior of the rocket’s thin-walled design (in a 3D case).
A critical aspect of this problem is the need to accurately represent the solid body, which, due to its significantly thin boundaries, behaves more like a shell rather than a traditional solid object. This necessitates the use of specialized shell element formulations in our numerical approaches to account for the unique stress and strain characteristics of such structures.
Additionally, incorporating adaptive mesh refinement and computational fluid dynamics (CFD) techniques will enhance the accuracy of the airflow representation, providing a detailed understanding of the aerodynamic forces acting on the rocket. Engaging in a comprehensive validation process against experimental data will also ensure the reliability of the model, allowing for improved prediction of the rocket’s performance during flight.
Ultimately, this combined approach will promote a more robust analysis of the rocket’s dynamics, facilitating better design choices and enhancing overall performance in real-world applications.
For this problem, I generated a dynamic hybrid mesh that combines orthogonal structured mesh elements with unstructured triangular elements for the finite element method, as shown in two figures below. By employing a novel dynamic mesh strategy, I successfully simulated the problem while significantly reducing CPU time. I will present this approach in a scientific paper. Once it is published, I will update this page with more interesting insights. Stay tuned!

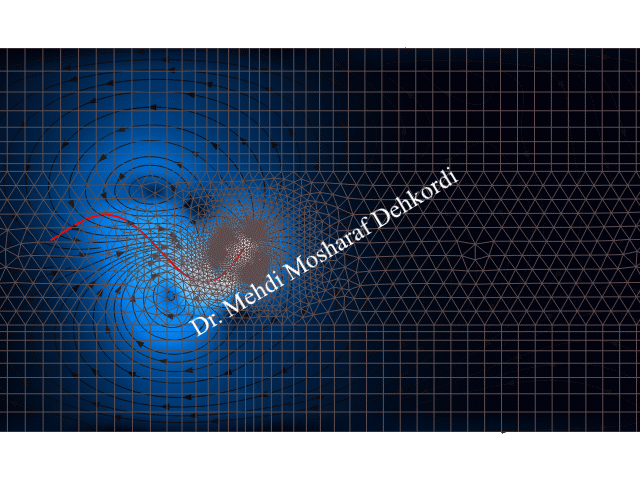
Numerical Results
Here, the normalized velocity field is presented along with streamlines at different times




Notes
This simulation presents a unique opportunity to delve into the fascinating interplay between solid objects and fluid mechanics. By visualizing and understanding the complex behavior of airflow around the rocket paper, we can contribute valuable insights to multiple fields, ultimately enhancing our design processes and technological advancements in aerospace applications
