Welcome to My Exploration of Phase Change Materials
Join me on a journey of discovery and innovation as we explore the importance of phase change materials (PCMs). The following problem aims to provide educators, researchers, and industry professionals with invaluable insights that expand the potential of PCMs in various applications. Let’s uncover new experiences together!
Problem Definition
In the pursuit of efficient energy management and effective thermal regulation, the investigation of Phase Change Materials (PCMs) has become fundamental for innovation across multiple industries. This example aims to examine the complex melting process of a PCM influenced by natural convection, specifically focusing on a PCM with an irregular solid shape immersed in its liquid phase within a rectangular domain.
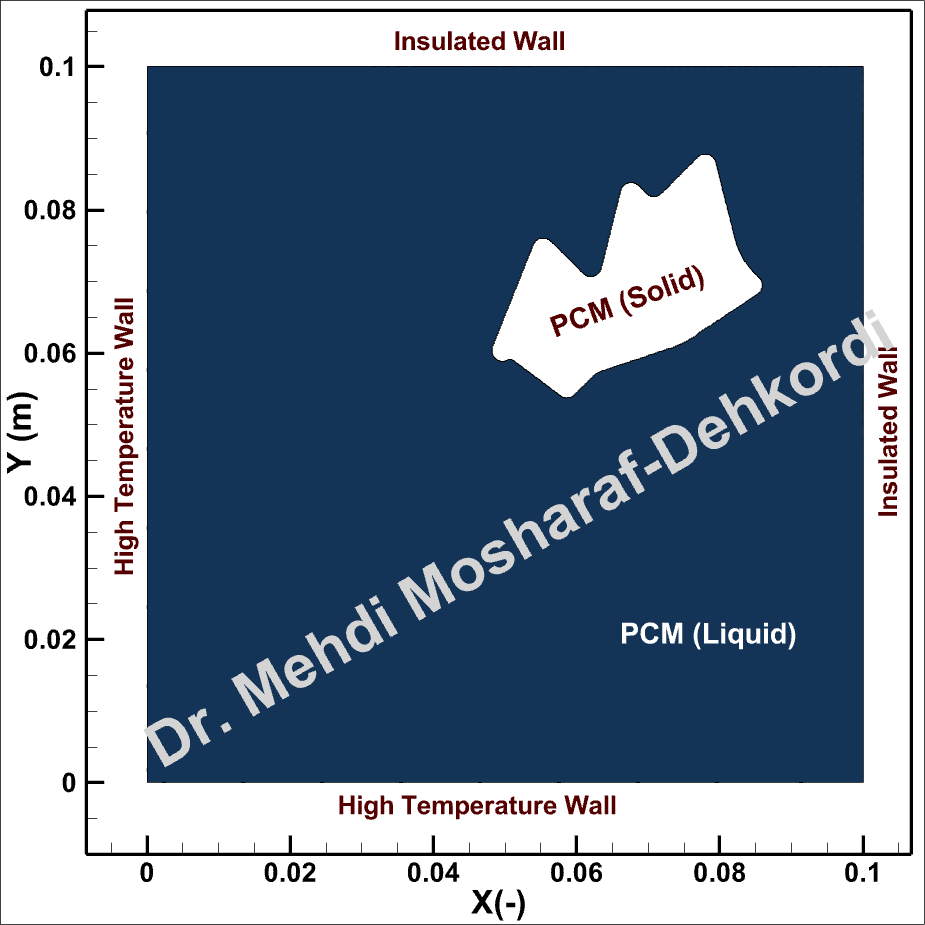
Assumptions, initial and boundary conditions
Thermal Setup:
Left and Bottom Walls: These walls are maintained at a constant high temperature (Th).
Remaining Walls: Thermally insulated to prevent heat exchange, ensuring a precise evaluation of the phase change dynamics.
Boundary Conditions:
No Slip Condition: A realistic scenario is established where the fluid velocity at the boundaries matches that of the wall, facilitating accurate fluid flow simulation. In this example, all domain walls are fixed.
Role of Gravity: Gravity is considered a significant factor affecting fluid motion, allowing for a detailed exploration of the interaction between the liquid PCM and its solid phase, thereby reflecting the intricate dynamics of natural convection.
Initial Condition:
The initial temperature distribution is configured such that the region within the solid PCM is below the melting temperature, while the surrounding area has a temperature exceeding the melting point. This setup is critical for analyzing the phase change process effectively.
It is assumed that the position of the immersed solid PCM is fixed and does not move due to the buoyant force.
Solution Approach and Computational aspects
Finite Element Approach: Even though by employing first-order elements, my method precisely models temperature distribution and fluid flow, effectively managing complex boundary conditions for enhanced accuracy.
Dynamic (Moving) Mesh Methodology: I accurately capture the intricate movements of phase boundaries during the phase change of PCM from solid to liquid. This methodology is crucial for tracking the solid region boundaries at each time step.
Natural Convection Dynamics: My approach utilizes the Bossiniuqe approximation to effectively model natural convection, even under density changes in the fluid due to thermal distribution, thermal expansion, and the related buoyancy forces. This allows me to capture the nuances of fluid behavior in complex thermal systems.
Numerical Results


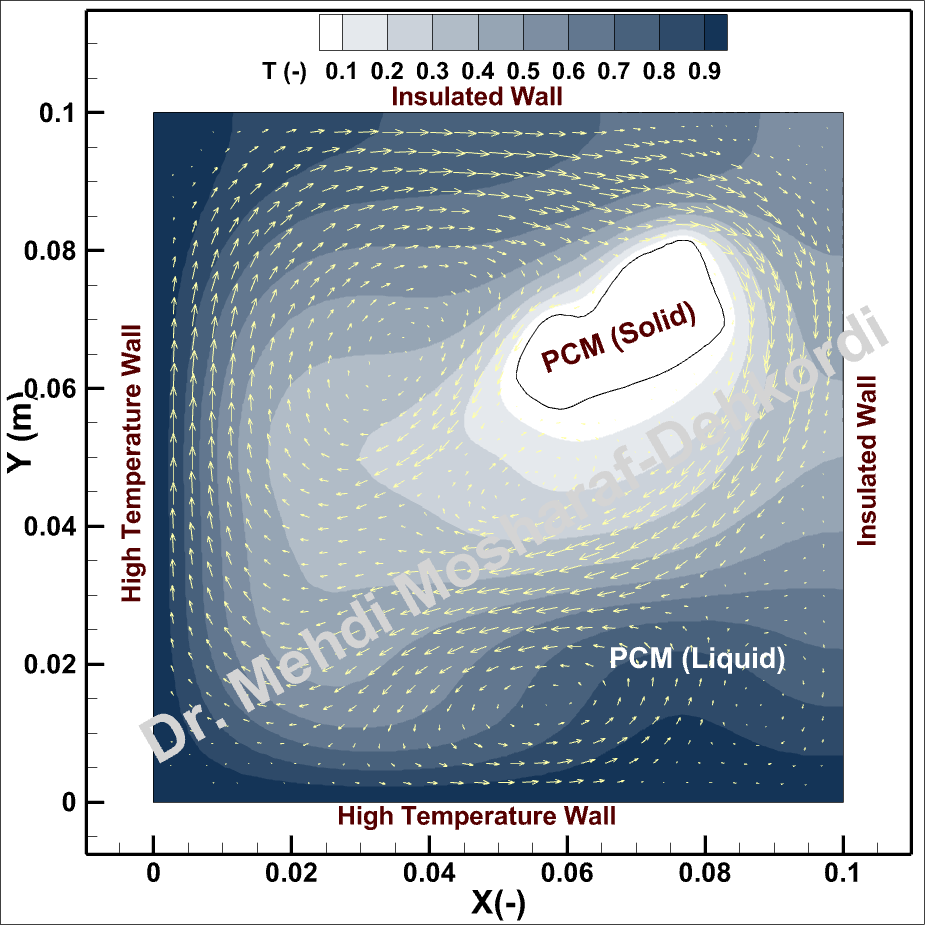
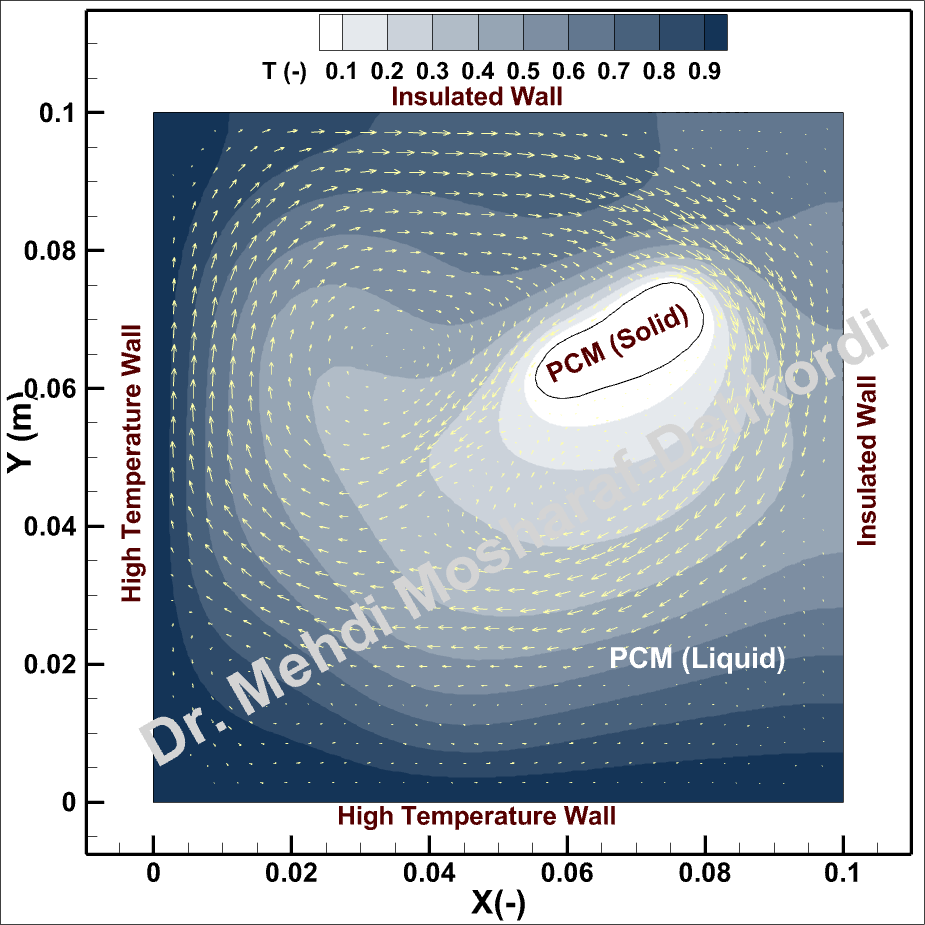

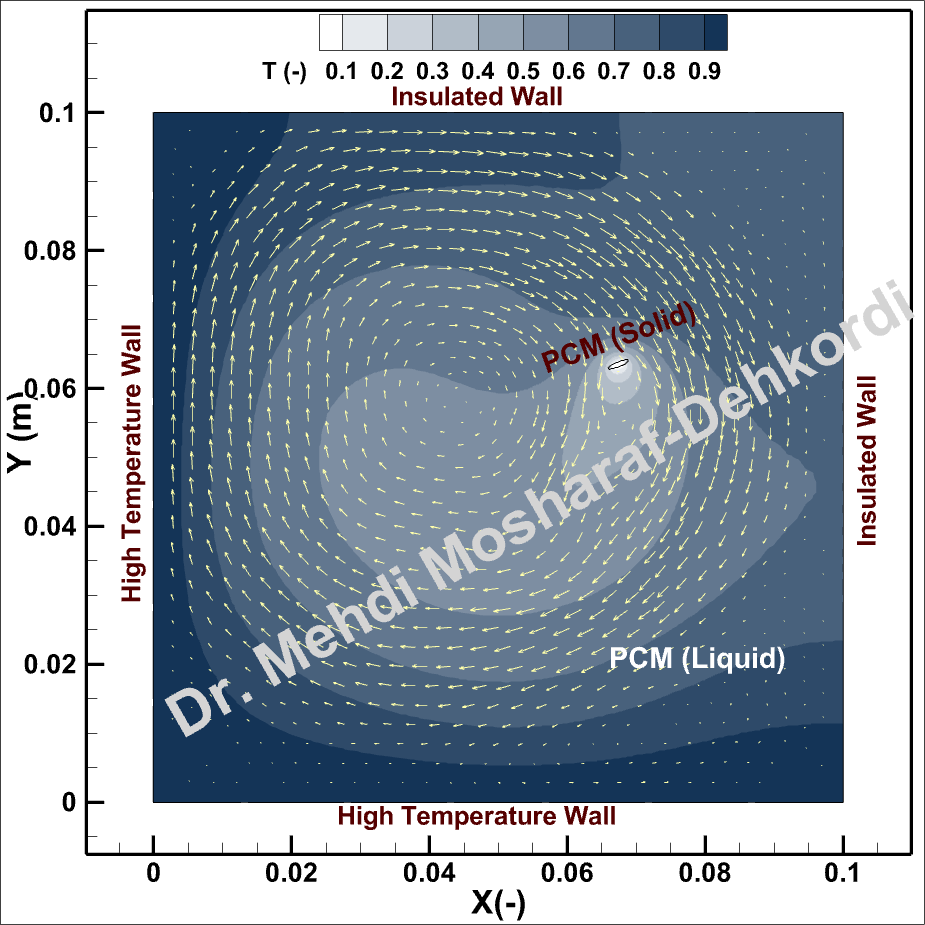

Importance
PCMs play a crucial role in several key areas:
Energy Storage: By enhancing the efficiency of thermal energy storage systems, PCMs allow for effective capture and release of energy during peak demand.
Building Efficiency: By regulating indoor temperatures, PCMs contribute to sustainable architecture and help reduce heating and cooling costs.
Electronics Cooling: Advanced thermal management in electronic devices ensures they perform optimally and last longer by effectively dissipating excess heat.
Temperature Control in Pharmaceuticals: Providing controlled environments for sensitive materials to maintain their efficacy throughout transportation and storage.
Enhanced Energy Solutions: As global energy demands rise, efficient materials like PCMs can significantly lower energy consumption and reduce environmental impact.
Cross-Disciplinary Applications: From sustainable engineering to healthcare, my research appeals to various industries aiming for innovative temperature regulation solutions.
Notes
Consistent initial-boundary conditions are crucial for successfully simulating problems involving phase changes.
In this problem, I simulated the melting process of phase change materials influenced by natural convection, aiming to uncover insights that could transform energy efficiency across various fields.
