Understanding the Dynamics of a Droplet in a Multiphase Fluid System
Importance
The study of droplet dynamics in multi-phase fluid systems is crucial for various industrial applications, including oil recovery, emulsification processes, and the design of chemical reactors. Understanding how droplets interact with different fluid layers can lead to improved efficiency in these applications, enabling better control of processes that rely on the behavior of fluids with varying densities.
Problem Definition
This problem investigates the behavior of an oil droplet immersed in water, particularly focusing on its interaction with a layer of light oil situated above the water. When the droplet is released, it experiences buoyancy forces that propel it upward through the water column. Upon reaching the light oil layer, the droplet encounters a negative buoyancy force, which slows its upward movement until it eventually reverses direction, descending back into the water. This cycle continues, with the droplet’s movement dampened gradually due to energy dissipation and fluid resistance.
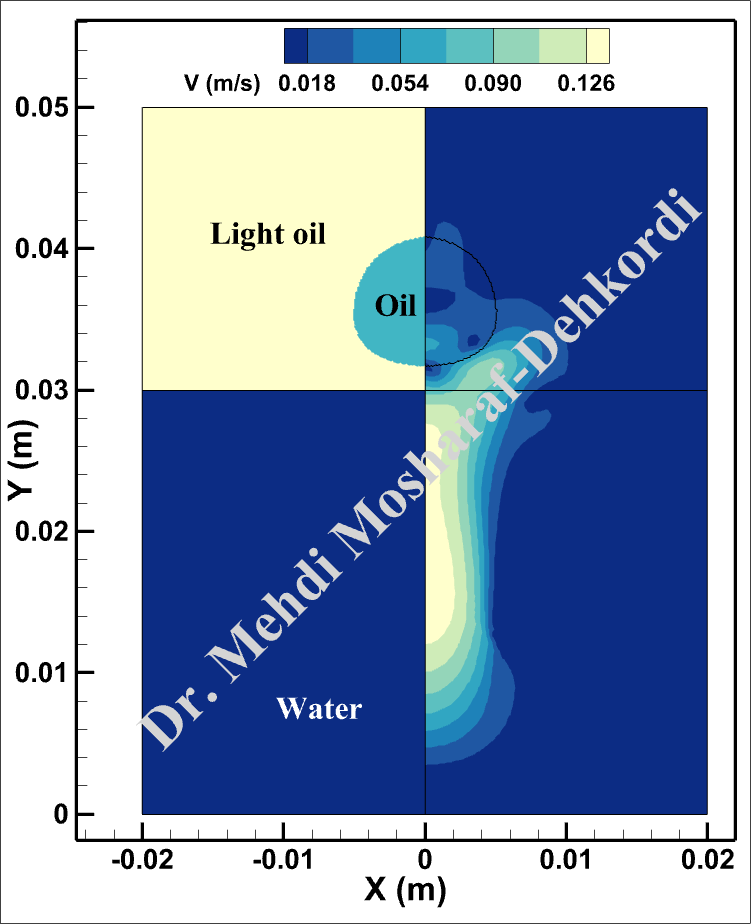
The computational domain is defined as a 2D axisymmetric rectangle, measuring 5 cm in height and 2 cm in width, as shown in the following figures. The droplet is initially modeled as a half-circle with a diameter of 1 cm, and its density is lower than that of water but higher than that of the light oil. This problem is numerically simulated in two different scenarios:
- Case 1: The movement of the water and light oil phases is neglected.
- Case 2: The interactions between the water and light oil phases are considered.


Assumptions
Thermal Setup
- The system is assumed to be isothermal, meaning that temperature variations do not significantly affect the fluid properties.
Boundary Conditions
- Fluid Interface: The interface between water, the droplet, and light oil is treated as a dynamic boundary, allowing for motion and interaction.
- No-slip Condition: At the walls of the rectangle, a no-slip condition is applied, meaning that the fluid velocity at the boundary equals zero.
- Pressure Boundary: The pressure at the top of the column is assumed to be atmospheric, whereas the lower boundary is at a specified depth that allows for appropriate fluid dynamics.
Initial Condition
- The droplet is initialized at the bottom of the domain in a half-circle shape (diameter = 1 cm) resting on the water surface before it begins its ascent due to buoyancy.
Solution Approach and Computational Aspects
The numerical simulation employs a finite volume approach to solve the governing equations of mass continuity and the Navier-Stokes equations. The level set method is utilized to accurately capture the interface dynamics among the three phases: the water, the oil droplet, and the light oil layer. The simulation is conducted in two different scenarios:
Case 1: The movement of the water and light oil phases is neglected.
Case 2: The interactions between the water and light oil phases are considered.
For both cases, the droplet movement over time is presented through animations that clearly depict its trajectory. Additionally, velocity magnitude plots are provided, showcasing lines that represent the different phases at various time intervals.
Numerical Results
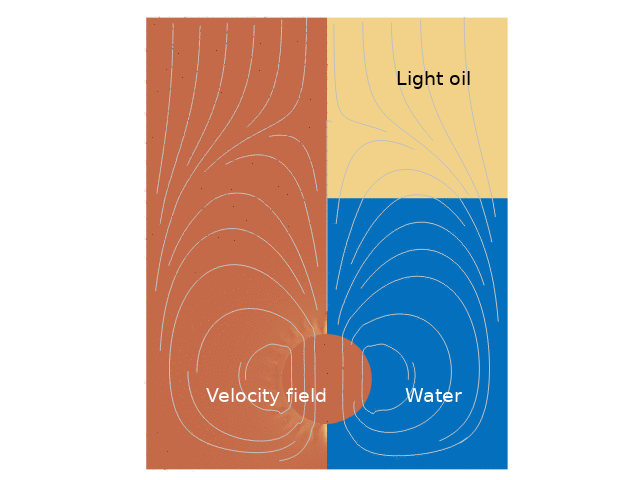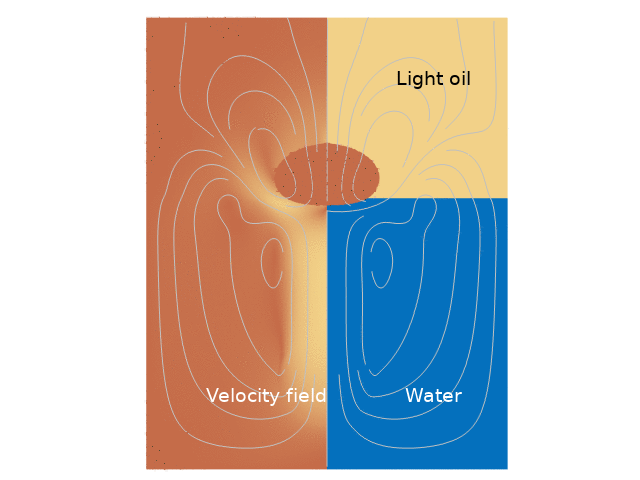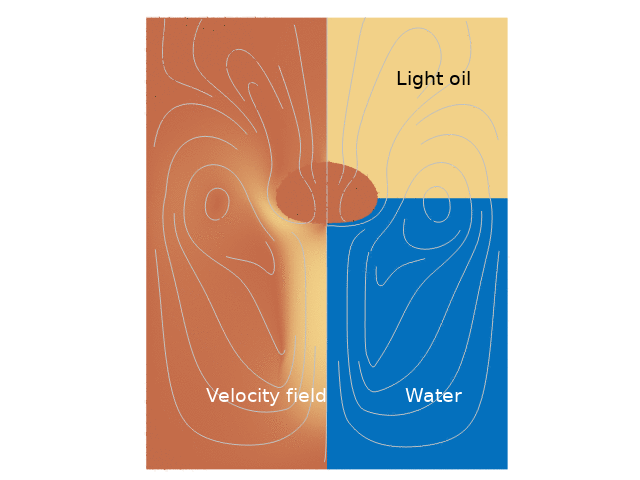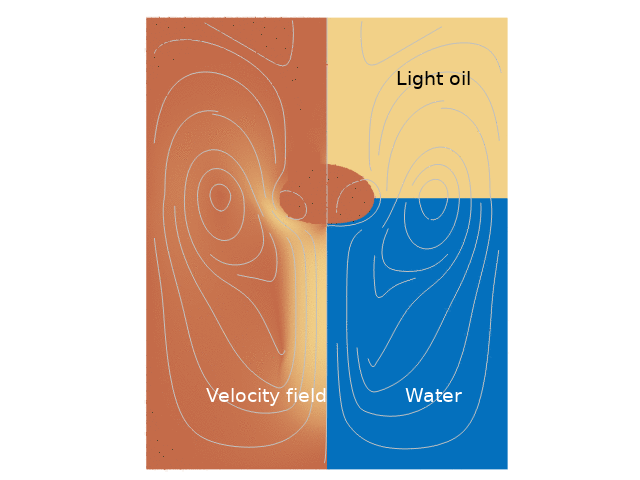
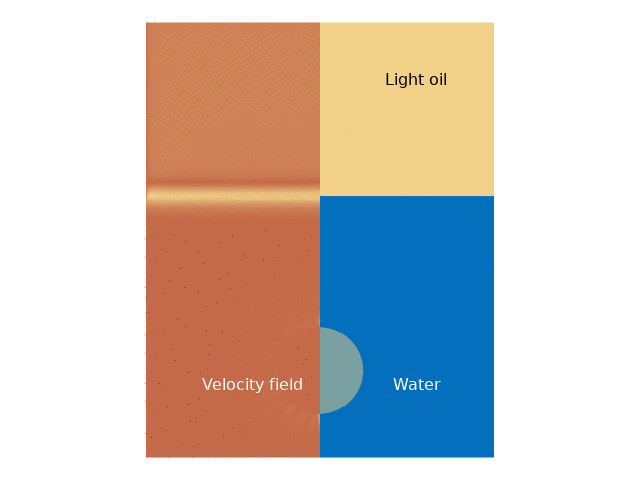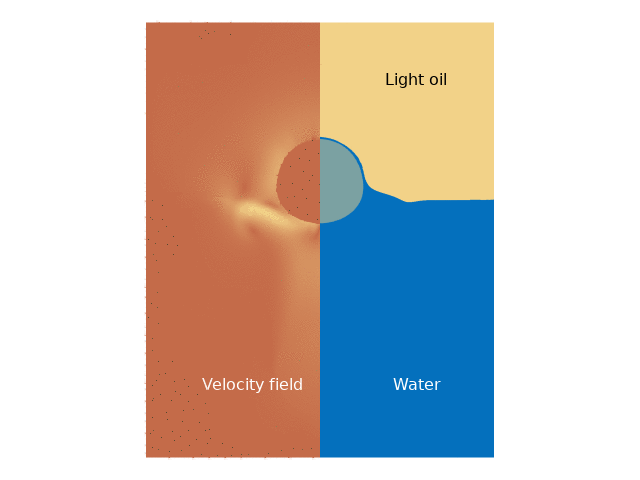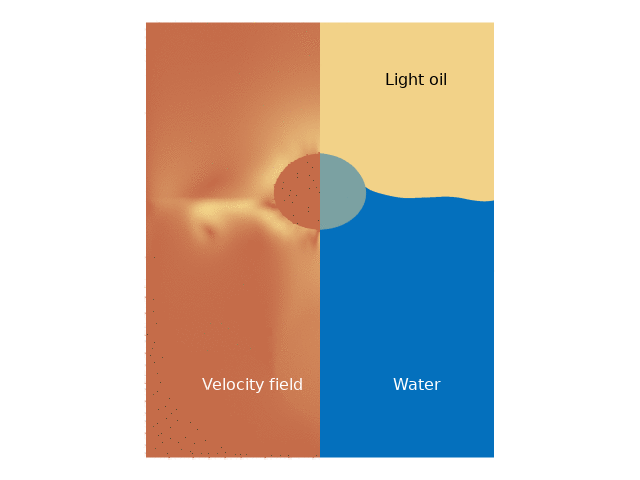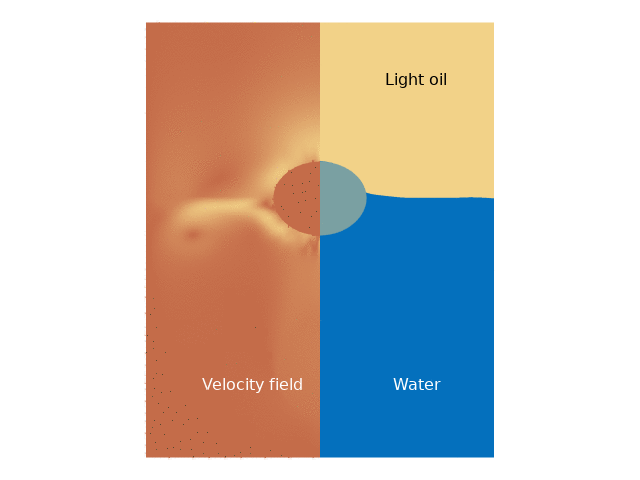
The results indicate a significant difference in droplet behavior depending on whether the interaction between the water and light oil phases is included. In the first case, the droplet experiences more pronounced buoyancy and downward motion upon entering water, whereas, in the second case, the interaction with the light oil layer introduces complex dynamics that dampen the upward velocity more significantly. The animations reveal that the droplet’s repetitive movement causes gradual stabilization, eventually leading to a predictable pattern of ascent and descent.











Notes
The simulation results contribute valuable insights into the impact of fluid interactions on droplet dynamics.
Future research directions may include exploring varying fluid densities and additional layers, as well as the effects of external forces, such as electromagnetic fields or varying temperatures.
These findings have potential implications in optimizing processes involving multi-phase systems in industrial applications.
