Welcome to My Exploration of Natural convection in porous media
Importance
Understanding natural convection in porous media is crucial for various engineering applications, including insulation systems, geothermal energy extraction, and the study of environmental processes. This simulation provides insights into the thermal and fluid dynamics, helping to optimize systems involving heat transfer in porous materials, which aims to provide educators, researchers, and industry professionals with invaluable insights that expand the potential of heat transfer in porous media in various applications.
Problem Definition
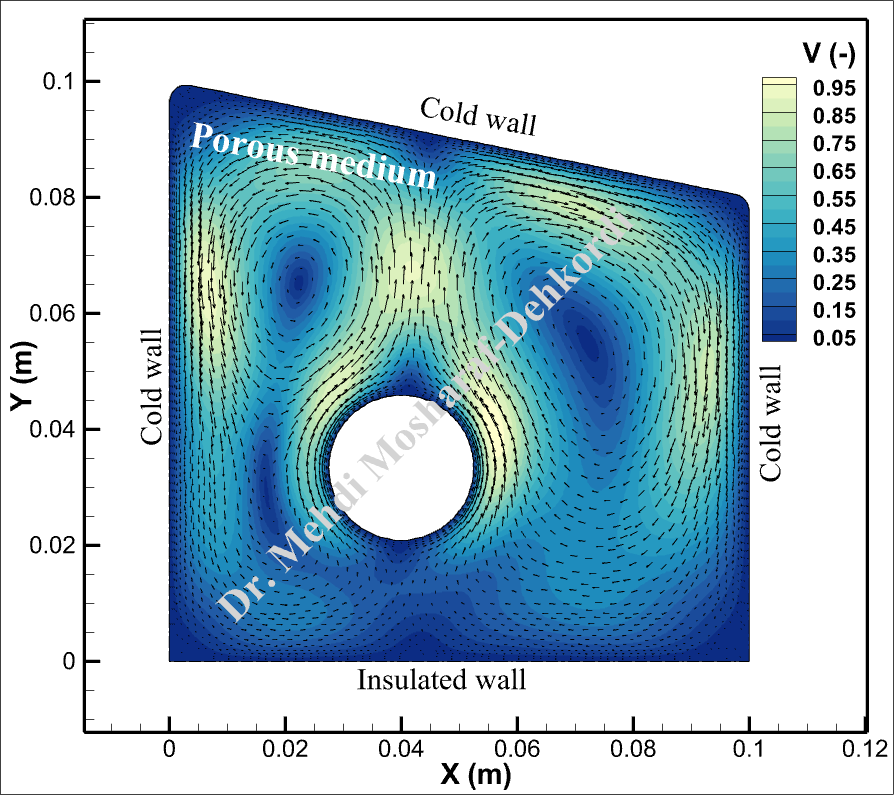
The problem is modeled as a 4-sided polygon shown below, where a circular hot surface is located inside. Three walls of the domain are maintained at a cold temperature, while the bottom wall is thermally insulated. The system is governed by transient natural convection, and the significant outputs of this simulation include velocity vectors, temperature distributions, and their corresponding animations with streamlines.
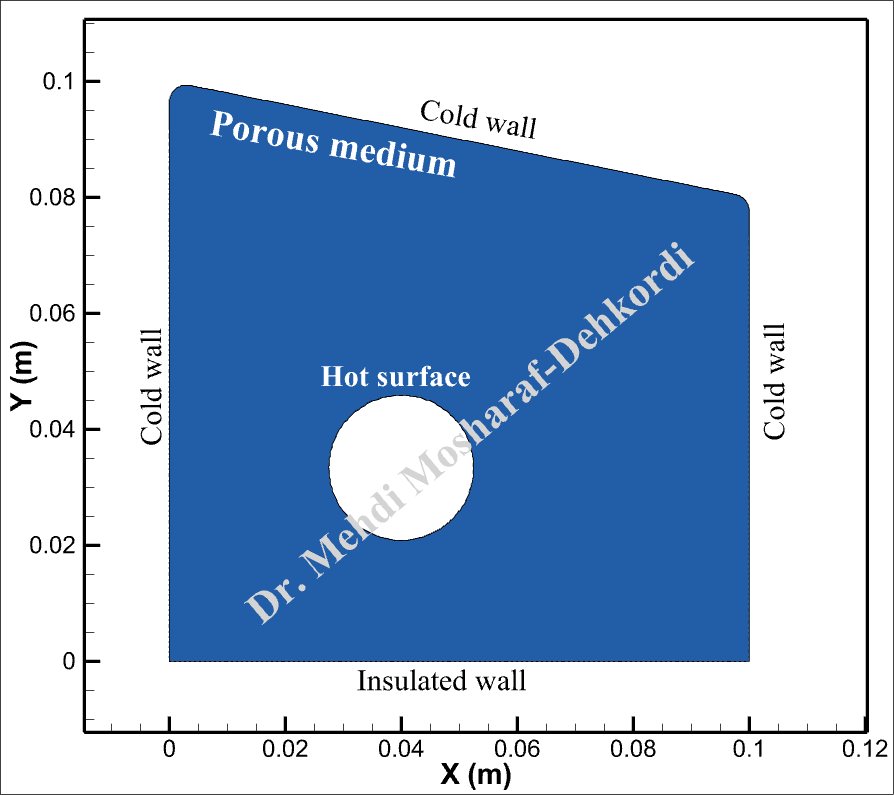
Assumptions, initial and boundary conditions
Thermal Setup:
- The porous medium is assumed to be homogeneous and anisotropic, which means varying conductive properties in different directions.
Boundary Conditions:
- Hot Surface (Circle): Maintained at a constant high temperature.
- Cold Walls (Three Sides): Kept at a constant low temperature.
- Insulated Bottom Wall: No heat transfer occurs.
- No-Slip Condition: Zero velocity at all walls, ensuring adherence to the boundaries.
Initial Condition:
- The entire domain starts at a uniform initial temperature, assumed to be equal to cold surface and fluid is at rest.
Solution Approach and Computational aspect
The solution employs the Brinkman Equation to model the momentum equation, delivering a comprehensive representation of natural convection within the porous medium. The reduced pressure formulation effectively captures the dynamics of fluid flow. Using the Finite Element Method (FEM), first-order elements are applied for all relevant variables, ensuring a sufficiently accurate solution while maintaining computational efficiency. Advanced visualization techniques translate the results into interpretable animations that showcase the velocity vectors and temperature distributions.
Numerical Results
The simulation results reveal intricate patterns of temperature distribution and fluid flow within the porous medium. The animations illustrate the dynamic interactions between the hot surface and surrounding cold walls, showing how natural convection evolves over time. Dimensionless Velocity vectors depict the flow direction and magnitude, while dimensionless temperature contours highlight the thermal gradients across the domain.
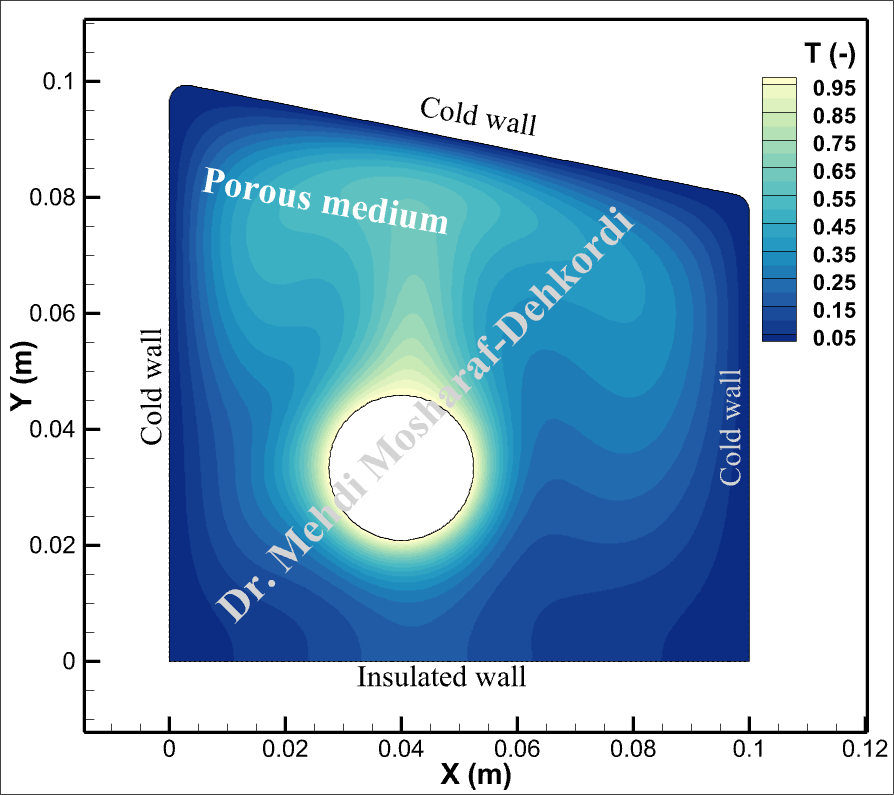
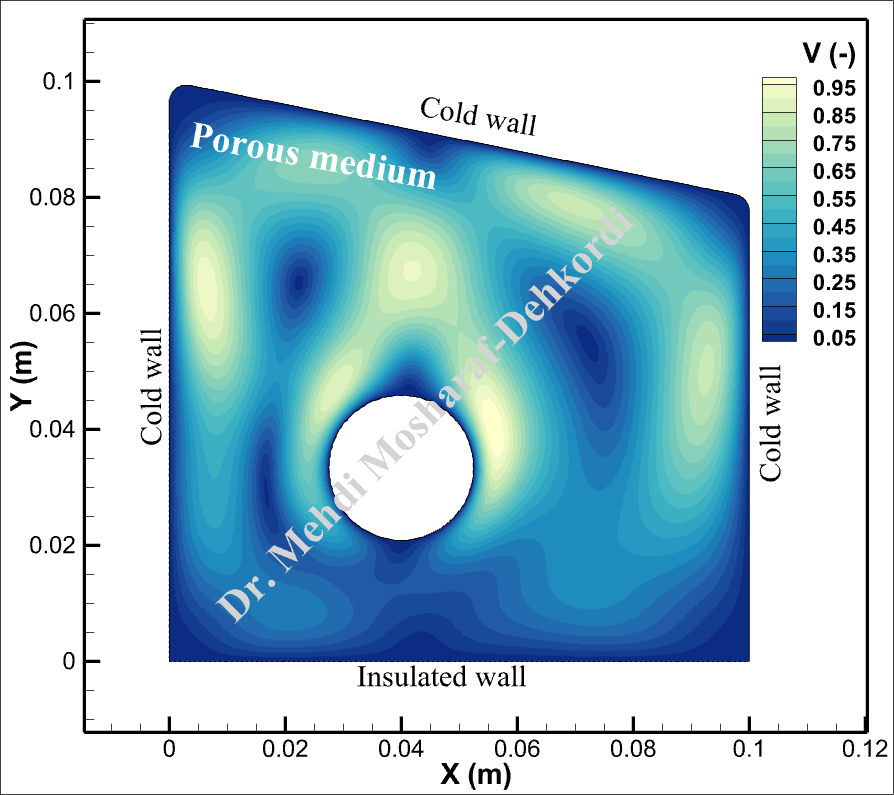

Notes
The findings could significantly impact designing effective thermal management systems, and further studies can expand upon these results by varying the material properties and geometric configurations. Comparing pore-scale and meso-scale of a related problem can provide valuable insights into porous media simulations.
